25 Basic Sets and Venn Diagram Tips and Formulae for BECE and WASSCE Exams
Venn diagrams are a powerful tool for visually representing relationships between sets, making them crucial for excelling in BECE and WASSCE mathematics and integrated science exams. Here are 25 essential tips and formulae to master:
25 Basic Sets and Venn Diagram Tips and Formulae for BECE and WASSCE Exams
Sets Basics:
- Definition: A set is a collection of objects (elements) that have something in common. {2, 4, 6} is a set of even numbers.
- Empty Set: A set with no elements is called an empty set, denoted by {}.
- Universal Set: A set containing all elements under consideration is called the universal set, denoted by U.
- Membership: An element belongs to a set if it satisfies the defining property. 5 ∈ {1, 3, 5} but 7 ∉ {2, 4, 6}.
- Cardinality: The number of elements in a set is its cardinality, denoted by n(A). n({a, b, c}) = 3.
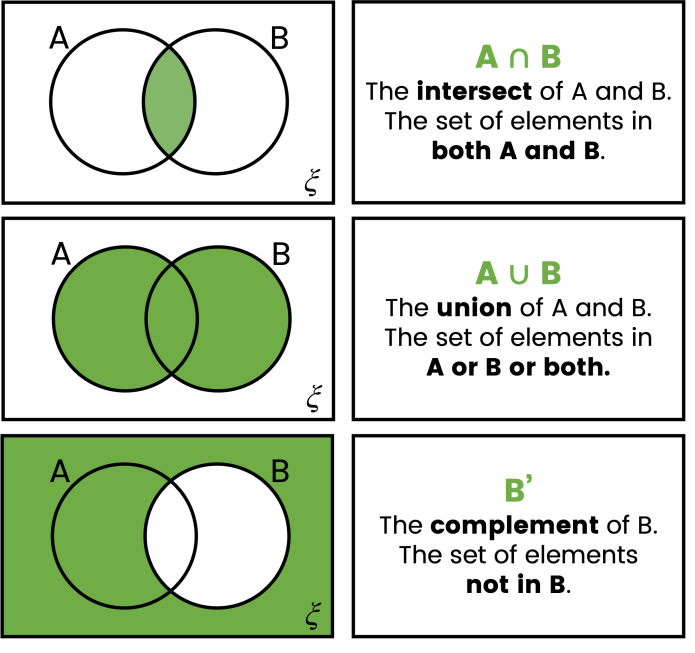
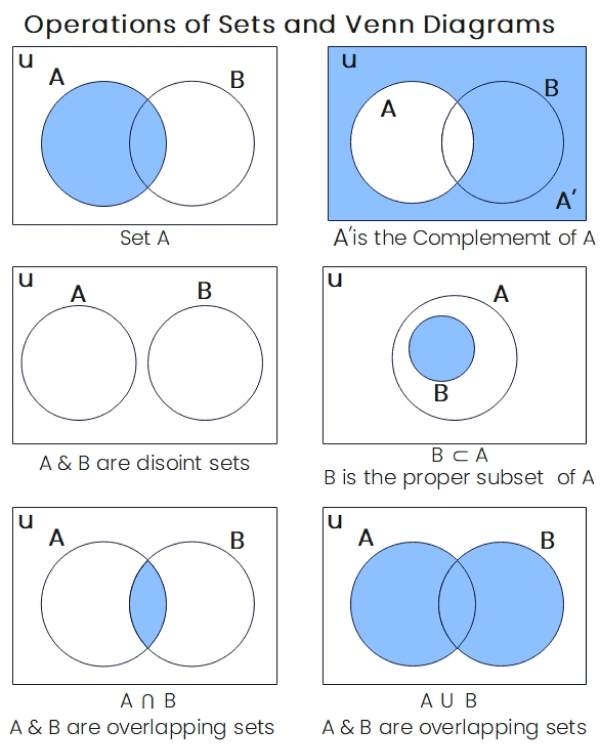
Venn Diagram Basics:
- Representation: Circles represent sets, overlapping areas show elements in both sets.
- Labeling: Clearly label sets and regions with their names or cardinalities.
- Shading: Shade regions to represent specific conditions (e.g., elements in A but not B).
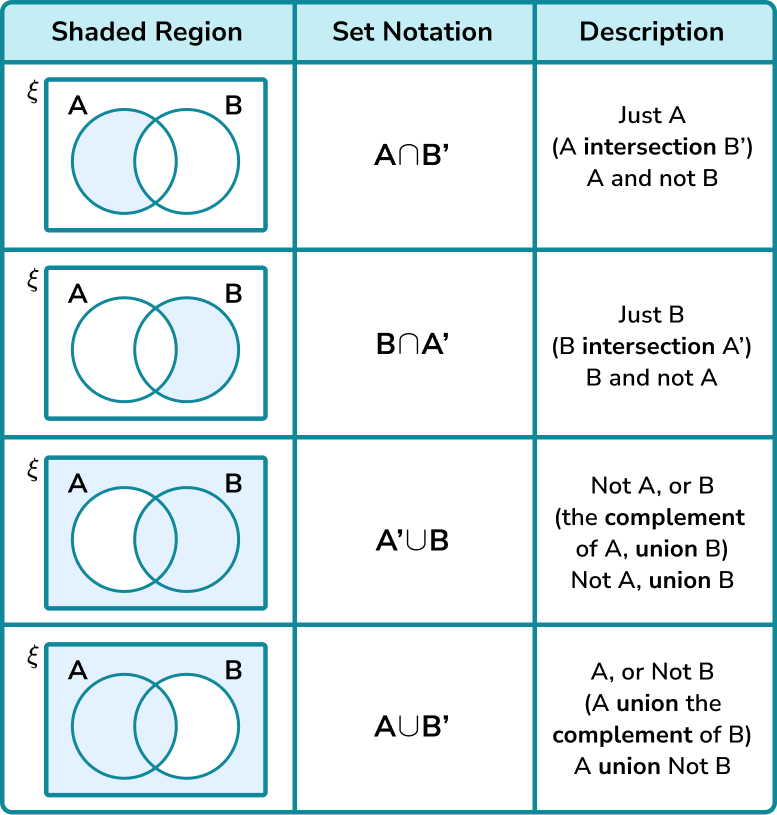
Set Operations:
- Union (∪): The union of A and B (A ∪ B) contains elements in A, B, or both.
- Intersection (∩): The intersection of A and B (A ∩ B) contains elements only in both A and B.
- Difference (∖): The difference of A and B (A ∖ B) contains elements in A but not in B.
- Complement (Ā): The complement of A (Ā) contains elements in U but not in A.
READ: 25 Essential Math Tips and Formulae for BECE and WASSCE Exams – GO HERE
READ: 25 Essential Integrated Science Tips and Formulae for BECE and WASSCE Exams – GO HERE
Venn Diagram Formulae (2 Sets):
- n(A ∪ B) = n(A) + n(B) – n(A ∩ B)
- n(A ∩ B) = n(U) – n(Ā) – n(B)
- n(Ā ∪ B) = n(B) – n(A ∩ B)
Venn Diagram Formulae (3 Sets):
- n(A ∪ B ∪ C) = n(A) + n(B) + n(C) – n(A ∩ B) – n(B ∩ C) – n(C ∩ A) + n(A ∩ B ∩ C)
- n(A ∩ B ∩ C) = n(U) – n(Ā) – n(B) – n(C) + n(A ∩ B) + n(B ∩ C) + n(C ∩ A) – n(A ∪ B ∪ C)
Tips:
- Read the question carefully: Identify the sets, operations, and conditions involved.
- Sketch a diagram: Draw a clear Venn diagram before calculations.
- Fill in known information: Shade or label regions with known cardinalities.
- Use formulae strategically: Choose the appropriate formula based on the information given.
- Double-check your work: Ensure calculations and shading are accurate.
Example:
A survey of 100 students reveals 45 like football, 30 like basketball, and 20 like both. How many like neither sport?
Solution:
- Draw a Venn diagram and label sets (F: football, B: basketball).
- Shade the overlapping region with 20 (students liking both).
- Fill in the total number of students (100) in the universal set.
- Apply n(Ā ∪ B) = n(B) – n(A ∩ B) to find students who like basketball but not football: n(Ā ∪ B) = 30 – 20 = 10.
- Apply n(Ā ∩ B) = n(U) – n(F) – n(B) + n(F ∩ B) to find students who don’t like either: n(Ā ∩ B) = 100 – 45 – 30 + 20 = 35.
READ: 25 Essential Math Tips and Formulae for BECE and WASSCE Exams – GO HERE
READ: 25 Essential Integrated Science Tips and Formulae for BECE and WASSCE Exams – GO HERE
Remember: Practice with various problems to solidify your understanding and application of these concepts. Good luck as you make good use of the 25 Basic Sets and Venn Diagram Tips and Formulae for BECE and WASSCE Exams.



 GES 2024-2025 Academic Calendar for Public Schools
GES 2024-2025 Academic Calendar for Public Schools  GES to recruit university graduates and diploma holders-GES Director General
GES to recruit university graduates and diploma holders-GES Director General  GES is expected to announce reopening dates for public schools today
GES is expected to announce reopening dates for public schools today  Dr. Bawumia’s Smart Phone Credit Will Take 125 Years To Repay: A Misleading Promise
Dr. Bawumia’s Smart Phone Credit Will Take 125 Years To Repay: A Misleading Promise  2024-2025 Report Card Grading, Student Attitudes, Interests and Conduct Samples for Teachers
2024-2025 Report Card Grading, Student Attitudes, Interests and Conduct Samples for Teachers  US Staffing Agencies Recruiting International Job Seekers With Work Visa Sponsorship
US Staffing Agencies Recruiting International Job Seekers With Work Visa Sponsorship  Buy 1 Gig MTN or Airtel Tigo data for only GHS6.00 not GHS17.00
Buy 1 Gig MTN or Airtel Tigo data for only GHS6.00 not GHS17.00