2023 WASSCE Elective Mathematics – July Elective Trial Mock Questions

2023 WASSCE Elective Mathematics – July Trial Mock Questions. Solce All these questions.
We also have our Elective Maths Home Mock Questions and Answers available for sale here – 2023 WASSCE Elective Maths Mock Questions and Answers (Pay and Download)
Paper One
SECTION 1
l. A binary operation * is defined on R, the set of real numbers, by a* b = a + b – 3.
Find the identity element.
- 3
- 2
- 0
- -3
2. Find the sum of the sequence 4, -2, 1, -½, …
- -3/4
- 3/4
- 8/3
- 8
3. Solve the equation 256(x+1) = 8(1-x2) .
- -1, -5/3
- -3/8, -5/3
- 8/3,3/5
- 8/3, 5/3
4. If a and f3 are the roots of x2 + 3x – 4 = 0, find the value of a2 + B2 – 3aB
- -11
- 20
- 21
- 29
5. Rationalize 1√3 − √2
- √3 − √2
- √3 − √23
- √3 + √22
- √3 + √2
6. If log5(6x + 7)-log56 = 2, find x.
- 2356
- 2616
- 3016
- 3316
7. The polynomial f(x) = x3 -4x2 + x + 8 is divided by (x – 2). Find the remainder
- 0
- 2
- 4
- 6
8. lf p x + 32x − 1 , express 2P + 13p + 1 in terms of x
- 4x − 55x − 8
- 4x − 55x + 8
- 4x + 55x + 8
- 4x + 55x − 8
9. Find the radius of the circle x2 + y2 +6x-4y-l2=0.
- 3
- 5
- 6
- 12
10. lf log10(x2) + log10(10x)=4, find the value of x
- -10
- -1
- 1
- 10
11. The remainder when the f(x)=5x3 + px3 -x + 10 1s polynomial divided by (x + 1) is 8. Find the value of p.
- 1
- 2
- 3
- 4
12. Evaluate ∫203x5 + 2x4− x3x3
- 8.0
- 10.0
- 10.2
- 12.0
13. If y = x2 – 2x – 3, calculate the minimum value ofy.
- -4
- -1
- 1
- 4
Two functions f and g are defined on the set R, of real numbers by f(x) = √x−1 and g(x) = x2 + 1.
Use this information to answer questions 14 and 15.
14. Find the inverse of f(x).
- x-1
- √x + 1
- √x2 + 1
- x2 + 1
15. Find f (g(2)).
- 1 –✓5
- -1 + ✓5
- ±2
- ±5
16. Find the coefficient of x2 in the expansion of (1 + x/4 )6.
- 15/16
- 15/8
- 15/4
- 15/2
17. Consider the statements:
p: All tall men are models
q: Dela is a tall man.
Which of the following is a valid conclusion from these statements?
- Dela may be a model
- Some models are tall.
- All models are called Dela
- Dela is a model
18 Evaluate tan45°+tan30°1−tan45°tan30°
- -2-✓3
- 2-✓3
- – 2 + ✓3
- 2 + ✓3
19. An arc of a circle of radius IO cm subtends an angle of 4.4 radians at the centre. Find the length of the arc.
- 12 cm
- 22 cm
- 44 cm
- 55 cm
20. Given that M = [3413], N = [8551] and P = [−173−2] find M + N -P
- [12232]
- [12236]
- [12262]
- [12266]
21. Find the gradient of the tangent of the curve y = x3 – 2x2 – x – 2 at the point (0, – 2).
- -2
- -1
- 1
- 2
22. Simplify 5nC25nP2
- 1/5
- 1/2
- 1
- 5
23. In a village 40% of the men are farmers. If 5 men are randomly selected from the village, what is the probability that exactly 4 men are farmers?
- 48/625
- 24/625
- 16/625
- 48/3125
24. If 3[2x] − [1−y4] = [3−2y1−2x] find the values of x and y.
- X = – 1, y = 2
- x=l,y=-2/3
- x =5/3, y = 2/3
- x= 2, y = -1
25. Find, correct to one decimal place, the angle between the vectors 2j and (-5i + 4j)
- 15.2°
- 25.2°
- 38. 7°
- 51.3°
26. Find with respect to x, the derivative of (3-5x2 )3
- -30x(3-10x2)2
- – 30x(3 – 5x2)2
- 30x(3 – 10x2 )2
- 30x(3 – 5x2 )2
27. Find the equation of the normal to curve y = x3 + 3x2– 4x + 1 through point (0, 1).
- 4y+x-4=0
- 4y-x-4=0
- y-4x+ 1 =0
- y-4x- 1 =0
28. If x = 3cosθ and y = 2sinθ, find x29 + y24
- 1
- 9
- 13
- 36
29. Which of the following vectors is parallel to the vector [2−4]
- [6−12]
- [−86]
- [34]
- [68]
30. Two fair coins are tossed together once Find the probability that no tail shows up.
- 3/4
- 2/3
- 1/2
- 1/4
31. For what values of x is 2x − 13x2 + 5x − 2
- -1/3 ,-2
- -1/3 ,2
- 1/3 ,-2
- 1/2,-2
2023 WASSCE Elective Mathematics – July Trial Mock Questions
32. In a family of 12 children, 8 play football, 7 play volleyball and 5 play both football and volleyball. Find the probability that a child selected at random does not play either of the two games
- 1/6
- 1/4
- 5/12
- 5/6
33. Forces (2i + 4j) N, (3i – 3j) N and RN act on a body. If the body remains in equilibrium, find R.
- (-5i – j)
- (-5i+ j)
- (5i – j)
- (5i + j)
34 A committee consisting of 2 girls and 3 · boys is to be formed from 6 girls and 9 boys. In how many ways can this be done, if one particular boy must be on the committee?
- 71
- 420
- 840
- 2002
A body starts from rest and accelerates at (2t + 5)ms-2, where t is the time in seconds. Use this information to answer questions 35 and 36.
35. Find the velocity of the body at t = 3 s.
- 2ms -1
- 6ms-1
- 11 ms-1
- 24 ms-1
2023 WASSCE Elective Mathematics – July Trial Mock Questions
36. Find the distance covered by the body in 3 seconds.
- 27.5 m
- 31.5 m
- 45.0 m
- 72.0 m
37. Given that a = i – j and b = 2i + 3j, find the unit vector along the vector b – a
- 1/√13(i+4j)
- 1/√13(4i – j)
- 1/√17(4i + j)
- 1/√17(i + 4j)
The table below shows the distribution of marks obtained in a test by 25 candidates. Use it to answer questions 38 to 40.
|
Marks |
20-39 |
40-59 |
60-79 |
80-99 |
|
Frequency |
2 |
8 |
10 |
5 |
38. What is the class mark of the modal class of the distribution?.
- 60.5
- 64.5
- 69.5
- 79.5
39. If a student is selected at random, what is the probability that she obtained at most 79 marks?
- 2/5
- 1/2
- 3/5
- 4/5
40. Find the mean of the distribution
- 63.3.
- 63.9
- 69.3
- 79.9
2023 WASSCE Elective Mathematics – July Trial Mock Questions
Paper Two
SECTION 2
l. A binary operation is defined on the set R of real numbers by
x * y = x2 – 2xy + y2, x, y ER
a) Find m such that 2 * -5 = ✓m
b) (n + 1)∗nn ,n ≠ 0
SHOW ANSWER
2. The normal to the curve y = 2x2 + x – 3 at the point (2, 7) meets the x-axis at point Q. Find the coordinates of Q.
SHOW ANSWER
3. If (x-2) is a factor of the polynomial f(x) = 4x3 – 19x2 + ax -14, find
a) the value of the constant, a;
b) the zeros of f(x).
SHOW ANSWER
4. Given that k(x2 – 10x – 2) + (2x2 + 1) = o, find the values of k for which the quadratic equation has equal roots.
SHOW ANSWER
5. A pupil tries to arrange the letters in the word D U C K L I N G S, taking four letters at a time. Find the number of ways of the arrangement if
a) any of the letters can be used;
b) it must begin with a vowel;
c) it must end with any of the letters K, N, G and S.
SHOW ANSWER
6. The distribution of the ages of 22 school children is shown in the table below.
|
Age(years) |
12-14 |
15-17 |
18-20 |
21-23 |
24-26 |
|
Frequency |
6 |
10 |
3 |
2 |
1 |
Using an assumed mean of 19, calculate, correct to two decimal places, the mean of the distribution.
SHOW ANSWER
7. Two bodies of masses 3 kg and 6 kg move towards each other with equal speeds 10 ms -1 and collide head-on. After the collision, the velocity of the 6 kg mass reduces by 40%. Find the change m momentum of the 3 kg mass.
SHOW ANSWER
8. If A(2, 6), B(2, 2), C(7, 3) and D(x, y) are the vertices of a parallelogram ABCD, calculate the coordinates of D.
SHOW ANSWER
9. a) The gradient function of a curve at any point (x, y) is px2 + 3x – 2, where pis a constant. If the curve passes through points (1, 0) and (-1, 8/3) find
i) the value of p;
ii) the equation of the curve;
iii) the coordinates of the maximum point on the curve.
b) An error of 9% is mad e in measuring the volume of a sphere. Find the corresponding percentage error made in measuring its radius.
SHOW ANSWER
10. a) Solve the following equations for values of θ, 0° ≤ θ ≤ 360°:
i) cos(θ + 30°) + cos(θ – 30°) = cos 30°.
ii) cos 2θ – cosθ = 0.
b) The sum of the first n terms of a series is 8n2 -4n.
i) Find the first three terms of the series.
ii) Show that the series is a linear sequence.
iii) Find the nth term of the series.
SHOW ANSWER
2023 WASSCE Elective Mathematics – July Trial Mock Questions
11. a) Solve √y+7 − √3y−2 = 1 b) Using the trapezium rule with seven ordinates, evaluate ∫301x2 + 1dx correct to two decimal places.
SHOW ANSWER
12. a) Write down the linear transformation defined by the matrices
P = [−123−4] and Q = [−4−7−52]
b) Find the inverse, p-1, of the linear transformation defined by the matrix P.
c) Find
i) PQ;
ii) the image of the point (4, I) under the transformation Q followed by P.
SHOW ANSWER
13. The table shows the distribution of marks obtained by some candidates in an examination.
|
Marks |
0-9 |
10-19 |
20-29 |
30-39 |
40-49 |
50-59 |
60-69 |
70-79 |
80-89 |
90-99 |
|
Number of candidates |
2 |
6 |
8 |
18 |
28 |
18 |
10 |
6 |
3 |
1 |
a) i) Construct a cumulative frequency table for the distribution.
ii) Use your table in (a)(i) to draw the cumulative frequency curve.
b) Use your curve in (a) (ii) to estimate, correct to one decimal place,
i) the upper quartile of the distribution;
ii) the lowest mark for a distinction, if I 0% of the candidates passed with distinction;
iii) the probability of selecting a candidate who scored between 52% and 65%.
SHOW ANSWER
14. The table below shows the values of two variables x and y
|
x |
1 |
1 |
1 |
1 |
2 |
2 |
2 |
2 |
3 |
3 |
3 |
3 |
4 |
4 |
4 |
4 |
5 |
5 |
5 |
5 |
|
y |
1 |
2 |
1 |
2 |
2 |
3 |
3 |
2 |
3 |
4 |
3 |
4 |
4 |
5 |
3 |
6 |
5 |
6 |
5 |
6 |
a) Plot a scatter diagram to represent the data.
b) i) Find x, the mean of x and y, the mean of y.
ii) Plot (~, y) on the scatter diagram.
iii) For each value of x, calculate the mean of the corresponding values ofy.
iv) Plot on the scatter diagram, the points in (b) (iii).
c) Draw the line of best fit to pass through the points plotted in (b)(iv)
d) Using your graph, find
i) the equation connecting x and y;
ii) the value of y when x = 4.
SHOW ANSWER
15. a) The probability that Isaka will be alive in 1O years time is 1/6 and the probability that Ashatu will live for the next 20 years is 1/3 . Find the probability that
i) Isaka will be alive in IO years time and Ashatu will die before the next 20 years.
ii) at least one of them will be alive in 8 years time.
b) Six fair coins of the same size are tossed once. Find, correct to three decimal places, the probability that
i) a head is obtained;
ii) at least four heads are obtained.
SHOW ANSWER
16. a) Find, correct to one decimal place, the angle between p = [3−1] and q = [34]
b) A body lying on a smooth horizontal surface is acted upon by forces 5 N, 7 N and 8 N as shown in the diagram.
i) Calculate, correct to two decimal places, the magnitude of the resultant force.
ii) If the body is of mass 1.2 kg. find its acceleration.
SHOW ANSWER
17. A uniform beam XY of length 6 m and mass x kg rests on two supports P and Q, where |PX| = 0.8 m and |QY| = 1.8 m. Masses of 12 kg and 15 kg are suspended at points A and B respectively, where |XY| = 1.7 m and |BY| = 0.4 m. If the reaction at P is 150 N and the system remains in equilibrium under the action of these forces, find
a) the value of x,
b) the reaction at Q.
[Take g = 10 ms-2 ]
SHOW ANSWER
18. a) A car of mass 1.5 tonnes travels on a straight and smooth road. It accelerates from a velocity of 45 kmh-1 to velocity of 110kmh-1 in 20 seconds. Given that the resistance to motion is 180 N, find the force that pulls the_car. [Take g = 10ms-2 ]
b) A particle ts thrown vertically upwards with a velocity of 25 ms-1 from a point 1.6 m abovt’ th~ ground.
Calculate
i) the maximum height reached;
ii) the time it takes to return to the pomt where it was thrown.
[Take g = 10ms-2
Send Stories | Social Media | Disclaimer
Send Stories and Articles for publication to [email protected]
We Are Active On Social Media
WhatsApp Channel: JOIN HERE
2024 BECE and WASSCE Channel - JOIN HERE
Facebook: JOIN HERE
Telegram: JOIN HERE
Twitter: FOLLOW US HERE
Instagram: FOLLOW US HERE
Disclaimer:
The information contained in this post on Ghana Education News is for general information purposes only. While we endeavour to keep the information up to date and correct, we make no representations or warranties of any kind, express or implied, about the completeness, accuracy, reliability, suitability or availability with respect to the website or the information, products, services, or related graphics contained on the post for any purpose.




 Ministry of Education Postpones Reopening Date of Basic Schools By One Week
Ministry of Education Postpones Reopening Date of Basic Schools By One Week 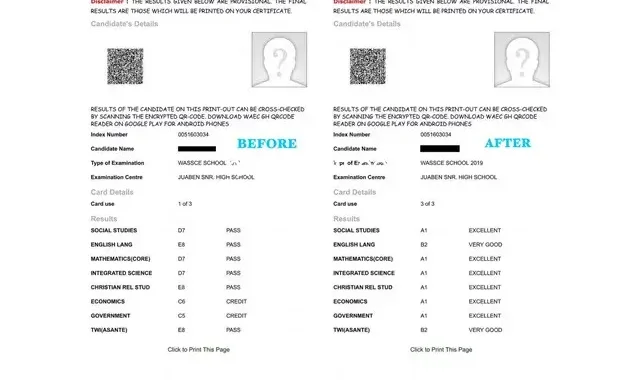 WASSCE Results Upgrading: Total Scam Or Something Worth Your Money?
WASSCE Results Upgrading: Total Scam Or Something Worth Your Money?  Teacher Unions Start Regional Demo With Volta Region On May 3rd
Teacher Unions Start Regional Demo With Volta Region On May 3rd  How to Apply to Any University in Ghana with D7 in WASSCE
How to Apply to Any University in Ghana with D7 in WASSCE  9 Challenges Shattering the Foundation of Ghana’s Education System
9 Challenges Shattering the Foundation of Ghana’s Education System  Old students build health centre for Awudome SHS
Old students build health centre for Awudome SHS